70以上 三角形 相似 問題 215972-三角形 相似 証明 問題
相似 問題 z 相似な図形の性質 z 相似の位置 z 相似比 z比の値 z 三角形の相似条件 z 三角形の相似条件を使った証明 z 相似の利用(測量) z 三角形と比 z 三角形と比の定理の逆 z 中点連結定理 z 平行線と比 z 三角形の角の二等分線と比直角三角形の中に正方形が入った問題は相似の三角形を作って解く 相似+三角形のテクニック3つ!の中学入試問題等 問題)浅野中学(問題文はワイが簡略化してます) 2つは同じ三角形です。defgは正方形です。正方形の1辺の長さは?相似な図形のかき方、三角形の相似条件や、相似を利用した距離や高さの求め方を練習していきます。 プリント6枚 中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード・印刷
相似三角形应用举例 Ppt课件下载 第一ppt
三角形 相似 証明 問題
三角形 相似 証明 問題-数学35章図形と相似「相似な図形」<準備問題①> 組 番 名前 1三角形の合同条件を書きなさい。 2次の図で,AB//CDのとき,次の問いに答えなさい。平面・相似・応用★問題 下の図は合同な直角三角形を2つ重ねた図形です。三角形ebfの面積を求めなさい。 問題文 ミスターnすぐに解けそうな問題ですが、一度、ハマるとなかなか解けない問題です。三角形の相似を意識して解けるかどうかです。まずはこ



相似三角形几年级苏科版九年级下6 7用相似三角形解决问题同步练习及答案 尚书坊
海城中学校の問題を少し変えて、(2)を追加しています。 解法a 三角形の問題ならば、相似三角形ができるように補助線を引いて、辺の比を求めるのが基本的考え方ですね。 rとqを通り、bcに平行な補助線を引けば、 abp、 apcそれぞれの相似形が見えます。相似比: ⇒2乗 面積比: そして、面積比を考えるときには次のことも覚えておきたい! このように、2つの三角形が相似でなかったとしても 高さが等しければ、 底辺の比 を見比べることで面積比を求めることができます。 相似なら、相似比の2乗答えは、 ずばり、 三角形 ADE A D E と三角形 CEG C E G の相似です。 一番はじめに注目した相似です。 相似比は 1 2 1 2 なので、 DE EG = 1 2 D E E G = 1 2 です。 F G F E = 1 4 F G F E = 1 4 と合わせると、下図のように長さをおけます。 より、底辺が 8x 8 x 、高
面積比の公式3選とは三角形 さて、今までの話を踏まえ、ここからは「 相似じゃない図形の面積比 」について考えていきます。 具体的には 高さが等しい三角形;三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは相似な立体の表面積・体積(1) 相似な立体の表面積・体積(2) 6 円 円周角と中心角(1) 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理
相似な図形と線分比と平行の関係、その計算方法と図形をとらえる視点について応用問題を含めて学習します。 三角形と線分比 平行線と線分比 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似 線分比と相似直角三角形の相似 相似の証明でも取り扱った「直角三角形の相似」です。 このページでは辺の長さや比を求めていきましょう。 相似な直角三角形が現れる図形として、最重要・最頻出のものを扱います! 直角である頂点から斜辺へ垂線を第5章 図形と相似 <前:L29 相似な図形とその性質 の問題 L30 三角形の相似条件 の解答:次> 練習問題1 以下の1~3の各組の三角形は相似である。 このとき、それぞれの相似条件を答えなさ




例析相似三角形中的面积计算问题 每日头条




等腰三角形的存在性問題 與相似三角形相結合 綜合性強 人人焦點
相似形であるとわかる条件が提示されている問題では、相似になっている三角形の3つの辺のうち、どこか1つでも比がわかれば面積比が計算できます。 相似比は底辺の比であり、高さの比でもあるため、 面積比は相似比の二乗 で求められます。三角形と四角形プリント 小学2年生の三角形と四角形プリントです。 こちらは基本的な 図形問題ではありますが、学校でも多くの時間をかけて授業していきます。 まだまだ先の話ですが今後、立方体・四角柱など3次元の図形を理解していく上での 基礎とまた、問題の解き方も簡単に解説していくので、ぜひこの記事を通してマスターしてくださいね! 目次 非表示 中点連結定理とは? 中点連結定理の使い方例題 中点連結定理の証明 証明①三角形の相似を利用 証明②平行四辺形の性質を



1



相似三角形中的辅助线 学生版 教师版 沃文网wodocx Com
学習1 直角三角形・図形の折り返しと相似 問題 右の図のような,∠a=90°三角形に限らず、どのような相似な図形においても、面積比は相似比の \(\bf{2}\) 乗となります。 相似の計算問題 それでは、ここまでに学んだ知識を活かして相似の計算問題に挑戦してみましょう。 計算問題①「三角形の相似比を求める」の直角三角形 abc があり, 頂点 a から辺 bc に垂線 ad をひく。 ⑴ 線分 cd の長さを求めよ。 ⑵ 線分 ad の長さを求めよ。 解 ⑴ abc ∽ dac だから ,ca :cd=bc acより 4:cd=5:4,cd=32 cm




关于正三形的相似问题 下列说法中 正确的个数为 所有的正三角形都相似 所有的正方形都相似 所有的等腰直角三角 三人行教育网 Www 3rxing Org



初中数学相似三角形知识点汇总 秦学教育
三角形eabと三角形ecdはチョウチョの形で、しかも辺abと辺cdは平行なので、相似です。 対応する辺の組でどちらも長さがわかっているのは、辺abと辺cdの組です。 辺ab辺cd=10cm5cm=21 よって、ふたつの三角形の相似比は21です。だから、辺ea辺ecも21です。証明 (合同・相似)が苦手な人へ 教遊者 IC Channel 198K subscribers Subscribe 中2,中3,受験生平行と合同,三角形と四角形,相似「証明 (合同・相似)が苦手な人へ90%以上の証明に使えるテンプレートと素材まとめ」デジタル板書データ Watch later




コンプリート 三角形相似問題 シモネタ



相似三角形的判定 2
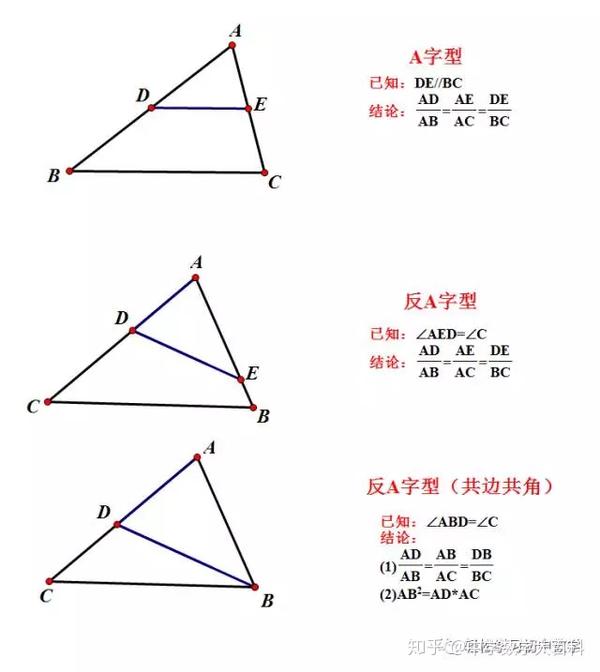



相似三角形的7大模型 知乎
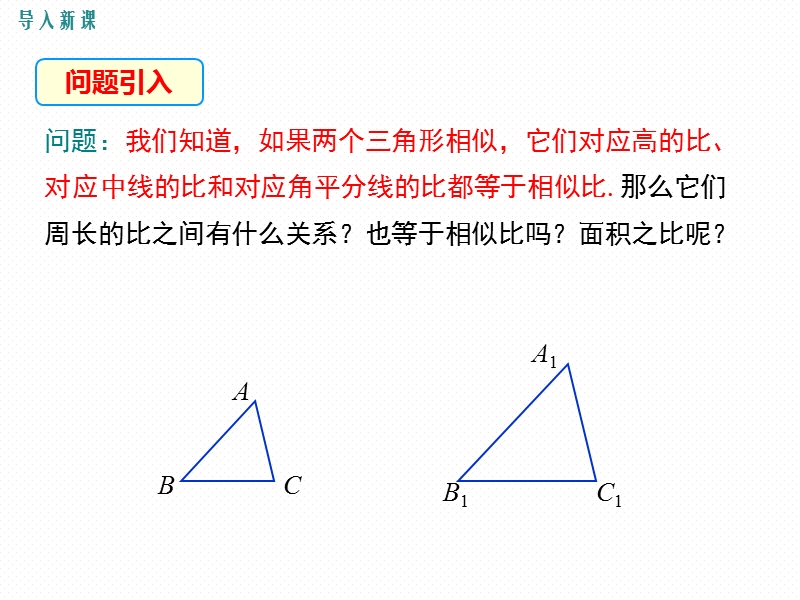



4 7相似三角形的周长和面积之比 第2课时 课件 七七文库www 77wenku Com




相似三角形的动点问题题型 整理 皮匠网



头条问答 初中的相似三角形 中考怎么考 有什么好的解题技巧 数理化培优课堂的回答 0赞
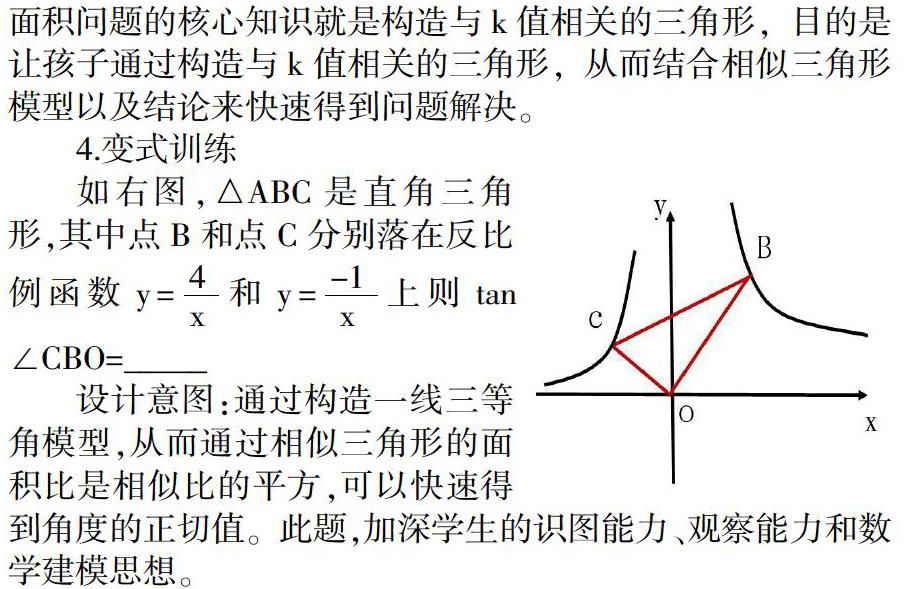



反比例函数与相似三角形问题 的复习课课例分析 参考网




相似三角形



相似三角形应用举例 Ppt课件下载 第一ppt



相似三角形几年级苏科版九年级下6 7用相似三角形解决问题同步练习及答案 尚书坊




几何问题之相似三角形 网易订阅
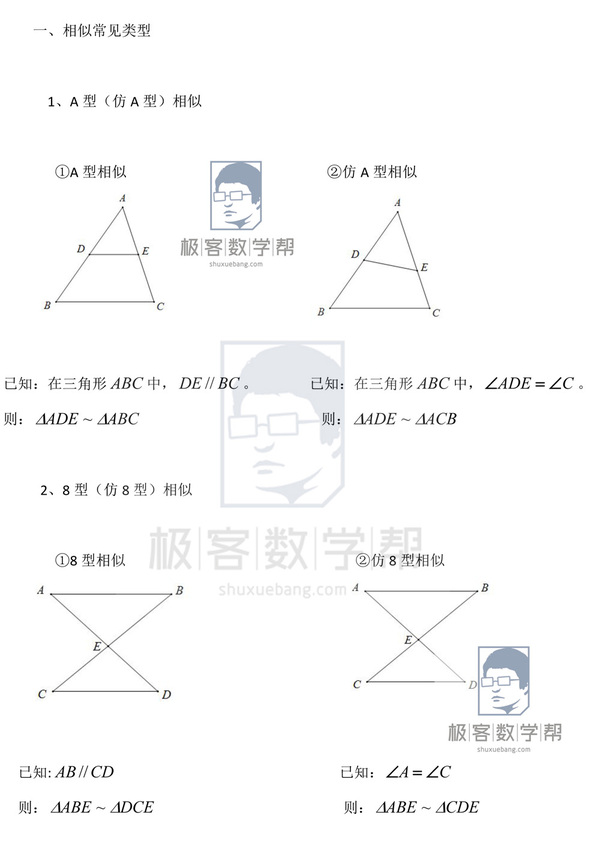



相似三角形搞不懂这几点 问题可就大了 教育频道 手机搜狐



数学名师 初中数学三角形相似问题这样解答就对了 冲刺数学满分




21中考数学压轴题题型 专题4二次函数与相似全等问题 含原卷及解析卷 教习网 学案下载



用相似三角形解决问题 禾教 初中数学互动课堂




部编版九年级数学下册相似三角形的判定课件ppt模板下载 熊猫办公



相似三角形问题 图片欣赏中心 急不急图文 Jpjww Com



27 2 3 相似三角形应用举例 人教版九年级下册数学电子课本 数九网




证明三角形相似的方法建议收藏 全等三角形证明中辅助线做法大全 相似三角形证明方法大全



數學名師 初中數學三角形相似問題這樣解答就對了 衝刺數學滿分 Zi 字媒體




中考真題詳解 因動點產生的相似三角形問題1 雪花新闻



跟三角形相似的图案 信息图文欣赏 信息村 K0w0m Com




中考數學 相似三角形搞不懂這幾點 問題可就大了 每日頭條




关于相似三角形的知识 相似三角形的相似比是什么 三人行教育网 Www 3rxing Org



腾讯视频




初中數學三角形相似問題這樣解答就對了 衝刺數學滿分 壹讀




高考考点题型精讲 物理 相似三角形法解平衡问题 教育 央视网 Cctv Com




中考 因动点产生的三角形相似问题



1
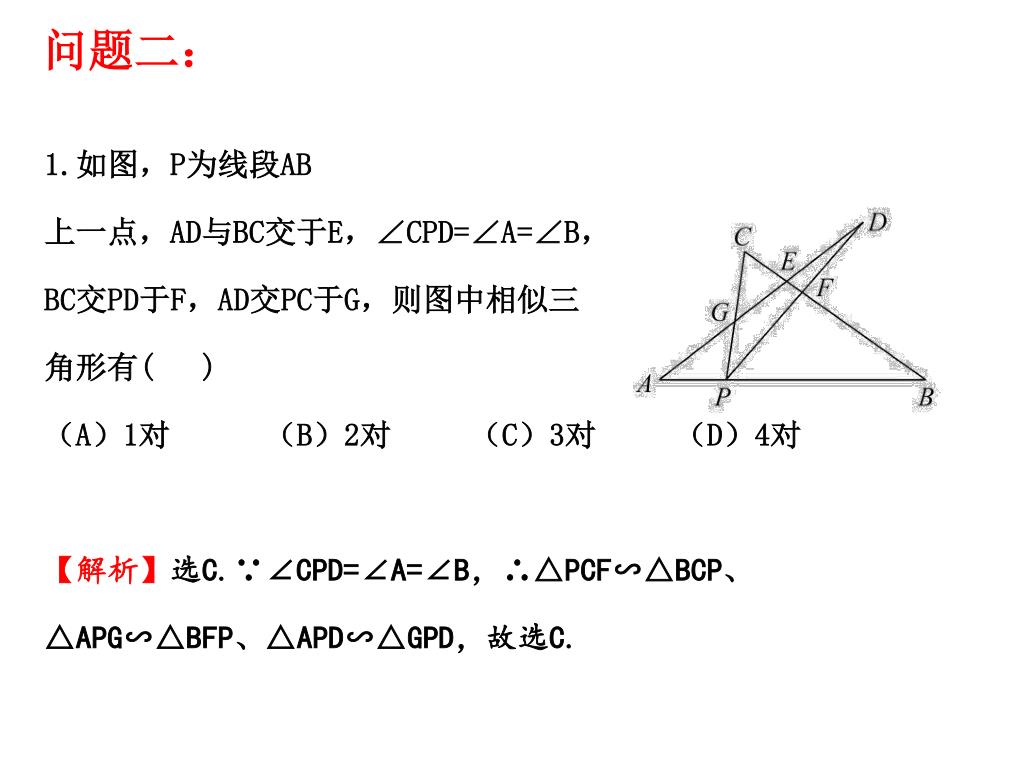



Ppt 中考第一轮复习 三角形相似powerpoint Presentation Id
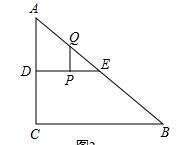



等腰三角形的存在性问题 与相似三角形相结合 综合性强 楠木轩



二次函数与相似三角形的综合问题 动态问题要以静制动 动中求静



1




相似形公式相似三角形計算公式 Zilhc



利用相似三角形解决圆中的线段问题 5 平行线型相似三角形例1 哔哩哔哩 つロ干杯 Bilibili




河南省濮阳市第级数学上册2 6 相似三角形的性质教学设计2 鲁教版 Doc 一八文库 M 184 Com
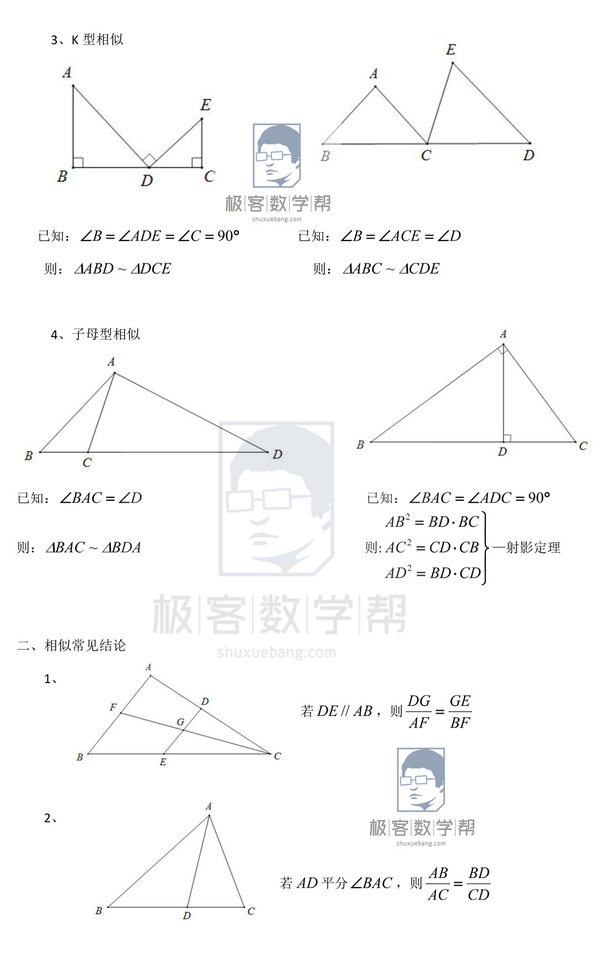



相似三角形搞不懂这几点 问题可就大了 教育频道 手机搜狐




九年级数学上册23 3相似三角形3相似三角形的性质教案 华东师大版 莲山文库



关于双动点问题的中考数学压轴题 辅助线构造相似三角形是关键 全网搜



初中数学 九年级数学下册 相似三角形知识总结及练习解析 进行




用相似三角形解决问题 巩固练习 基础



中考数学相似三角形经典练习15题 吃透15题 相似没问题 中考 学习资料大全 免费学习资源下载




几何问题之相似三角形 网易订阅



课程信息 本讲教育信息 一 教学内容 相似三角形和三角形相似的条件 1 了解相似三角形 相似比的含义 2 掌握两个三角形相似 的判断条件 并能够运用三角形相似的判断方法解决一些简单的问题 二 知识要点 1 相似三角形 1 相似三角形 对应角



相似三角形的性质 图形的相似ppt 第2课时 第一ppt



图形变化中一脉相承的全等与相似问题 6 3相似图形 初中苏科版13版 数学中国网 Mathschina Com



行测几何问题 相似三角形 图片欣赏中心 急不急图文 Jpjww Com



相似三角形综合题 含中点问题 整理了多种方法 计算量很大 初中数学 学习资料大全 免费学习资源下载



打印预览



用相似三角形对应高的比等于相似比解决实际问题 哔哩哔哩 つロ干杯 Bilibili



三角形相似中考真题 西瓜视频搜索



腾讯内容开放平台



4 7 第2课时相似三角形 的周长和面积之比 免费资源共享课件巴巴www Kejian Com公众号kejianbaba打包 Ppt 课件巴巴kejian Com 课件巴巴kejian Com



初一数学题相似三角形 信息图文欣赏 信息村 K0w0m Com




27 2 2相似三角形应用举例第2课时 Ppt 云豆网



27 2 相似三角形 人教版九年级下册数学电子课本 数九网
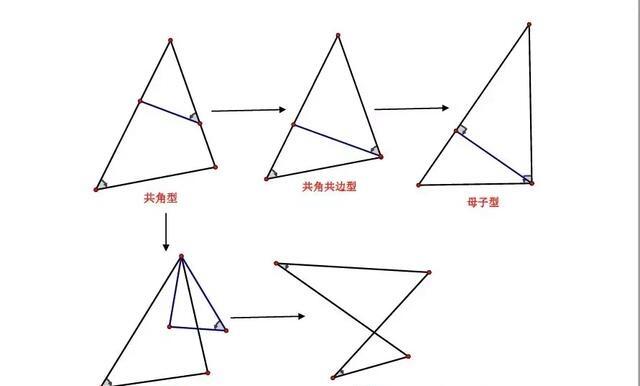



中考 因动点产生的三角形相似问题



腾讯视频



相似三角形的存在性问题解题策略 三部曲 统统都三步 初中数学 学习资料大全 免费学习资源下载



相似三角形 维基百科 自由的百科全书



初二数学问题 相似三角形的应用 狠急 图片欣赏中心 急不急图文 Jpjww Com




第二十七章相似相似三角形的判定第4课时两角分别相等的两个三角形相似 Ppt Download



课题 相似三角形判定1的应用的探索 备课吧



梯形相似定理 西瓜视频搜索



模型 相似三角形模型解析及辅助线作法梳理




九级数上册相似三角形的性质相似三角形中的开放性问题素材 新版 青岛版下载 Word模板 爱问共享资料



头条问答 初中的相似三角形 中考怎么考 有什么好的解题技巧 7个回答



掌握这些 相似一眼搞定 相似三角形的基本模型四射影定理型 好看视频



呼和浩特 相似三角形開放和幾何動態問題應用方法 雪花新闻




相似三角形的性质 图形的相似ppt 第2课时 下载 牛二ppt




相似三角形应用举例 九年级下册ppt课件 第27 2 4课时 Mac下载




二次函数压轴套路 1 相似三角形存在性问题 3326学习网




中考数学 三角形证明 题型总结 4




相似三角形的动点问题题型 整理 皮匠网



线段乘积问题必然与相似三角形有关 遇到了数学



头条问答 初中的相似三角形 中考怎么考 有什么好的解题技巧 数理化培优课堂的回答 0赞




相似三角形定义和性质 相似三角形的性质有哪些 三人行教育网 Www 3rxing Org



几何中的压轴题热点 掌握好相似类动点综合问题




相似三角形模型讲一线三等角问题讲义解答 豆知网



三角形动点问题带答案 搜狗图片搜索



数学 相似三角形系列03 面积比问题



数学 相似三角形系列03 面积比问题



初中数学 相似三角形判定定理证明浅见 来说说你的方法吧 知乎



1



相似三角形模型 万图壁纸网



4 4相似三角形的性质极其应用一 Ppt 沃文网wodocx Com




全国初中数学竞赛辅导第三十六讲 相似三角形 一 北师大版下载 Word模板 爱问共享资料
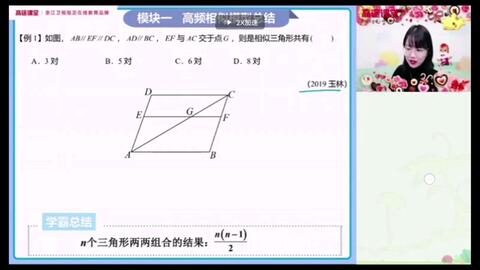



秋季数学第九讲例题一相似三角形计数问题 哔哩哔哩 Bilibili



相似三角形基本模型 宁夏初中数学 微信公众号文章阅读 Wemp




中考真題詳解 因動點產生的相似三角形問題1 雪花新闻



相似三角形的问题 图片欣赏中心 急不急图文 Jpjww Com




解读相似三角形经典图形 参考网



中考中常见的角的存在性问题 新闻时间




中考數學 相似三角形搞不懂這幾點 問題可就大了 Itw01




用相似三角形解决问题 巩固练习 提高
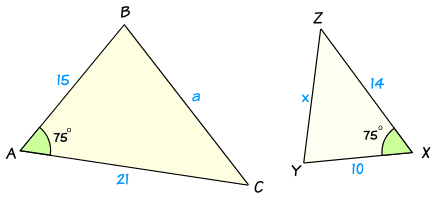



相似三角形的判定




常见三角形相似图形 相似三角形基本图形有哪些 三人行教育网 Www 3rxing Org




初中数学 相似三角形 全等三角形 手机网易网
コメント
コメントを投稿